A case where prospective matching may limit bias in a randomized trial
Cohort 연구의 경우 (전향적 연구)
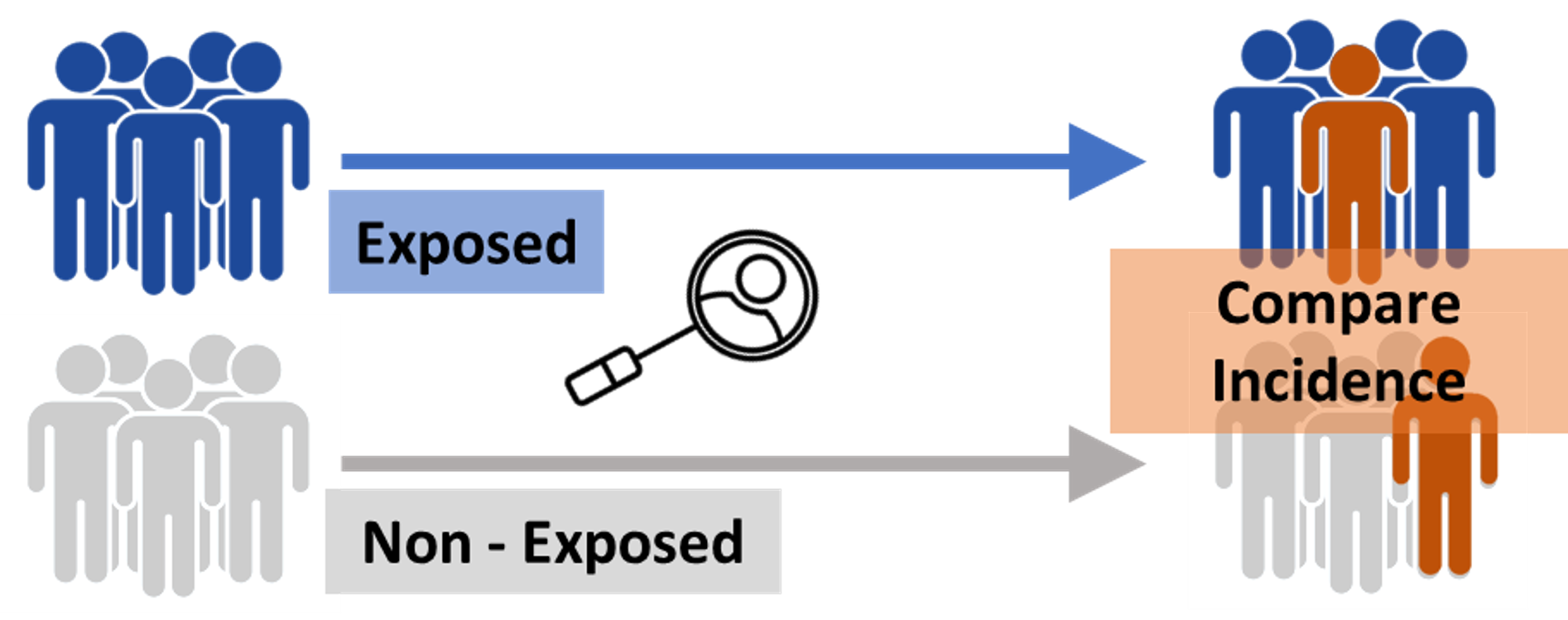
전향적 연구는 연구 시점에서 요인(치료, 위험인자)이 있는 사람과 없는 사람을 모아서, 결과 발생을 현 시점에서 시간의 경과와 더불어 추적해 가는 방법이다. 위험인자, 예후의 해석에 적합하다. Bias가 적은 것이 장점이지만 수고와 시간이 많이 걸린다.
Case Control 연구의 경우 (후향적 연구)
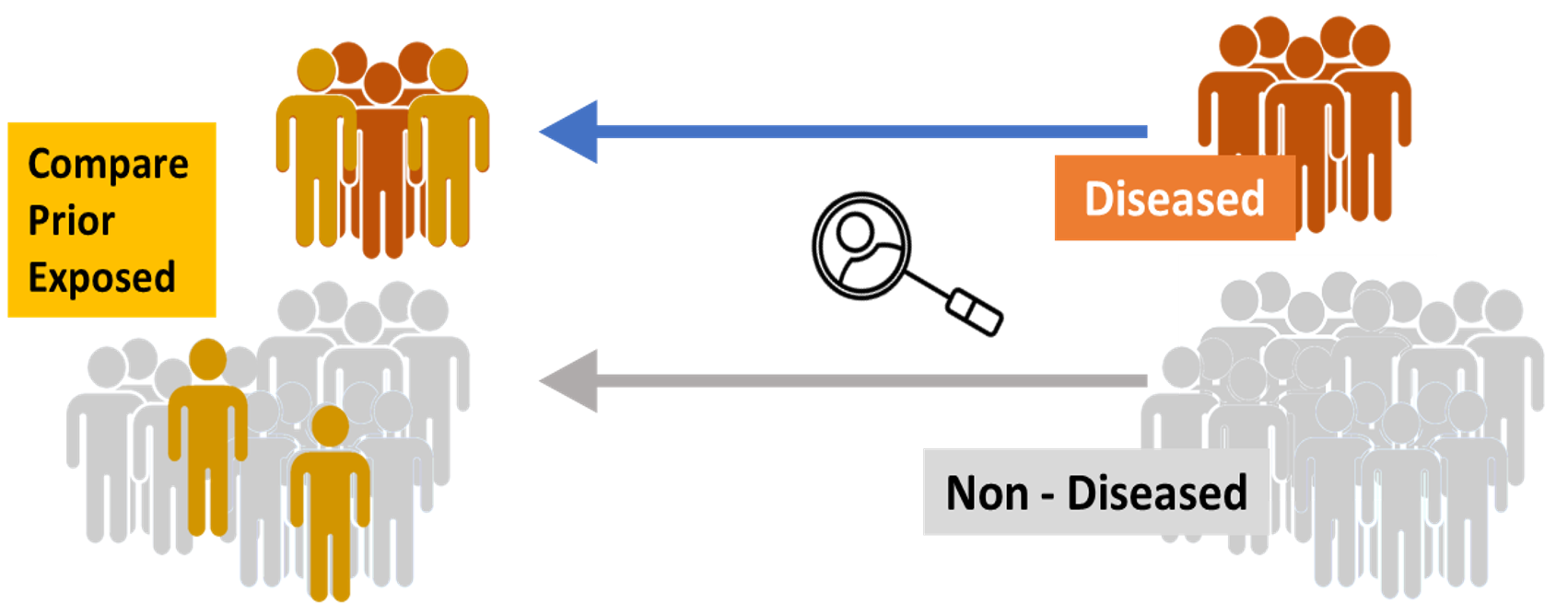
후향적 연구는 현재의 결과에서 시작되어 시간을 거슬러 올라가서 과거 요인의 유무를 해석하는 방법이다. 인과관계 발견에 적합하고, 노력이 적게 들지만, 연구자가 임의로 환자를 선택하게 되기 쉬워서 bias가 커지는 결점이 있다.
Case 군과 control 군의 base characteristics가 맞지 않음.
Case 군의 임상적 특징을 갖는 대상을 control 군 내에서 골라 Baseline 특성을 맞추어 주는 작업이 필요
If not, 선택 편향(selection bias) 발생
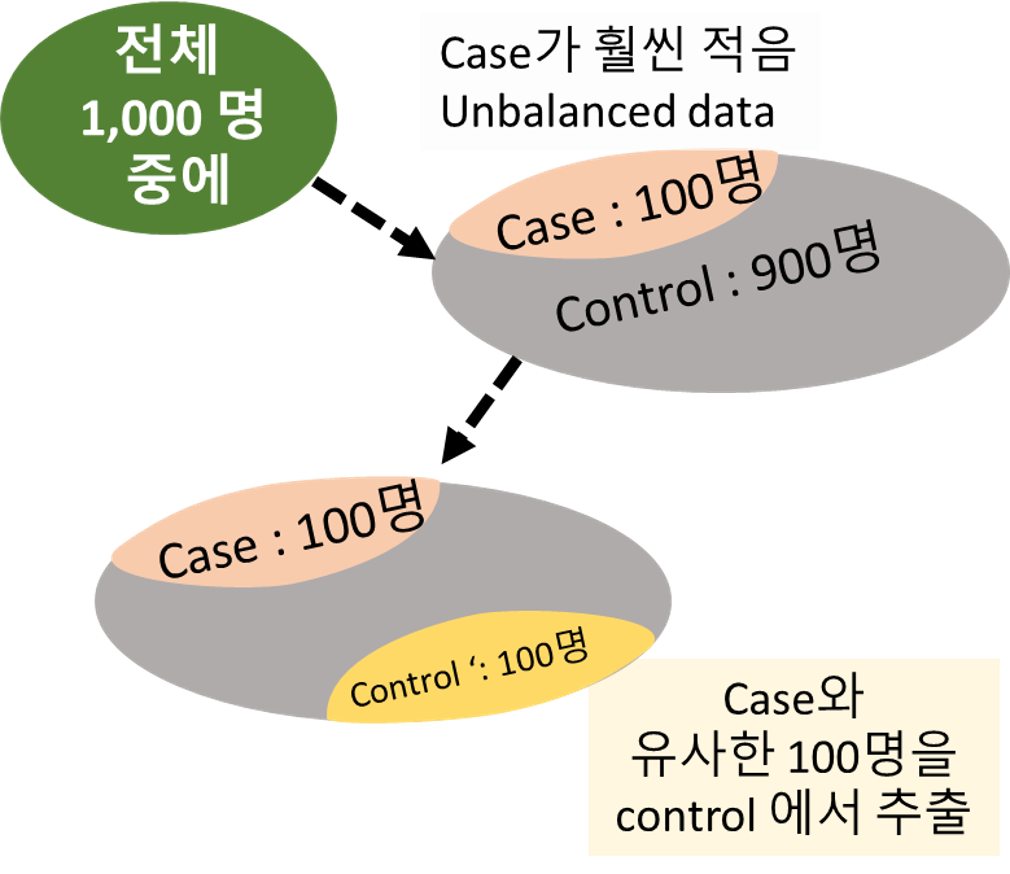
Matching의 필요성 예시
- 과연 control을 어떻게 설정할 것인가? *
Ex) 경구피임약이 유방암에 미치는 영향을 조사 시
- Case: 유방암이 발생한 여성
- Control : 유방암이 발생하지 않은 모든 여성
어린 초등학생들도 control 에 포함되어야 할까?
공변량(Covariate)들의 수준을 맞추어 통제한 후, 특정 독립변수가 종속변수에 미치는 영향의 정도를 제대로 파악할 수 있도록 하는 방법 : “ PSM “
(공변량은 여러 변인들이 공통적으로 공유하는 변량을 의미)
Article summary : The matching strategy
Analysis is important, but study design is paramount.
- 데이터에서 한 사람을 추출하여 나머지 사람들과 매칭시켜본다.
매칭 시에 고려되는 공변량 : 연구자의 생각에 기초하여 선정
such as age, gender, and one or two other relevant baseline measures.
2-1) 만약 매칭되는 사람이 없다면, 그 사람은 연구에서 제외.
2-2) 매칭되는 사람이 있다면, 첫 번째 개인은 therapy 그룹으로, 매칭된 사람은 control 그룹으로 배정
- 모든 사람이 matched되었거나, unmatched 그룹으로 할당될 때 까지 반
Library
library(dplyr)
library(data.table)
library(wakefield)
library(ggplot2)
library(knitr)
library(Matching)
- Matching Library
Multivariate and Propensity Score Matching with Balance Optimization
Data generation
300명의 simulated data를 생성 , ID와 성별(남자 70%, 여자 30%)과, 20세 부터 65세까지의 연령, BMI는 평균 25, 분산 3인 normal 분포 따르도록 생성
set.seed(1227)
dsamp <- r_data_frame(n = 300,
id,
sex(x = c(0,1),
prob = c(0.7,0.3),
name = "female"),
age(x = 20:65,
name = 'Age'),
Scoring=rnorm(300,25,3))
colnames(dsamp) <- c("ID","female","Age","BMI")
dsamp$BMI <-round(dsamp$BMI, 2)
dsamp$female <- as.numeric(dsamp$female)-1
dsamp <- dsamp %>% as.data.table()
dsamp %>% head %>% kable()
| ID | female | Age | BMI |
|---|---|---|---|
| 001 | 0 | 52 | 25.63 |
| 002 | 1 | 50 | 26.81 |
| 003 | 1 | 32 | 24.09 |
| 004 | 1 | 59 | 21.79 |
| 005 | 0 | 49 | 24.88 |
| 006 | 0 | 62 | 25.93 |
The matching algorithm
dsamp[, rx := 0]
dused <- NULL
drand <- NULL
dcntl <- NULL
set.seed(1227)
while (nrow(dsamp) > 1) {
selectRow <- sample(1:nrow(dsamp), 1)
dsamp[selectRow, rx := 1]
myTr <- dsamp[, rx]
myX <- as.matrix(dsamp[, .(female, Age, BMI)])
match.dt <- Match(Tr = myTr, X = myX,
caliper = c(0,0.5,0.5), ties = FALSE)
# Ideally, we would want to have exact matches,
# but this is unrealistic for continuous measures.
# So, for age and BMI, we set the matching range to be 0.5 standard deviations.
# (We do match exactly on gender.)
if (length(match.dt) == 1) { # no match
dused <- rbind(dused, dsamp[selectRow])
dsamp <- dsamp[-selectRow, ]
} else { # match
trt <- match.dt$index.treated
ctl <- match.dt$index.control
drand <- rbind(drand, dsamp[trt])
dcntl <- rbind(dcntl, dsamp[ctl])
dsamp <- dsamp[-c(trt, ctl)]
}
}
Treatment 그룹에 할당된 데이터
drand %>% group_by(female) %>% summarize(mean_of_BMI = mean(BMI), count=n()) %>% kable
| female | mean_of_BMI | count |
|---|---|---|
| 0 | 25.21000 | 102 |
| 1 | 24.96757 | 37 |
Control 그룹에 할당된 데이터
dcntl %>% group_by(female) %>% summarize(mean_of_BMI = mean(BMI), count=n())%>% kable()
| female | mean_of_BMI | count |
|---|---|---|
| 0 | 25.23196 | 102 |
| 1 | 24.88054 | 37 |
만들어진 데이터 형태
drand %>% head()%>% kable()
| ID | female | Age | BMI | rx |
|---|---|---|---|---|
| 119 | 0 | 32 | 23.91 | 1 |
| 212 | 1 | 39 | 20.36 | 1 |
| 245 | 0 | 21 | 28.34 | 1 |
| 036 | 1 | 23 | 23.35 | 1 |
| 086 | 1 | 37 | 21.66 | 1 |
| 113 | 0 | 35 | 22.65 | 1 |
dcntl %>% head()%>% kable()
| ID | female | Age | BMI | rx |
|---|---|---|---|---|
| 100 | 0 | 32 | 23.93 | 0 |
| 256 | 1 | 36 | 20.05 | 0 |
| 257 | 0 | 24 | 28.42 | 0 |
| 186 | 1 | 20 | 23.29 | 0 |
| 211 | 1 | 35 | 22.00 | 0 |
| 260 | 0 | 35 | 22.96 | 0 |
treatment 그룹과 control 그룹의 짝을 연결
mtanum이라는 변수를 이용
dused는 매칭되지 않은 데이터
drand$matnum <- c(1:dim(drand)[1])
dcntl$matnum <- c(1:dim(dcntl)[1])
dused1 <- dused
dused1$matnum <-NA
tt <- bind_rows(as.data.frame(drand),as.data.frame(dcntl))
tt %>% arrange(matnum) %>% head %>% kable()
| ID | female | Age | BMI | rx | matnum |
|---|---|---|---|---|---|
| 119 | 0 | 32 | 23.91 | 1 | 1 |
| 100 | 0 | 32 | 23.93 | 0 | 1 |
| 212 | 1 | 39 | 20.36 | 1 | 2 |
| 256 | 1 | 36 | 20.05 | 0 | 2 |
| 245 | 0 | 21 | 28.34 | 1 | 3 |
| 257 | 0 | 24 | 28.42 | 0 | 3 |
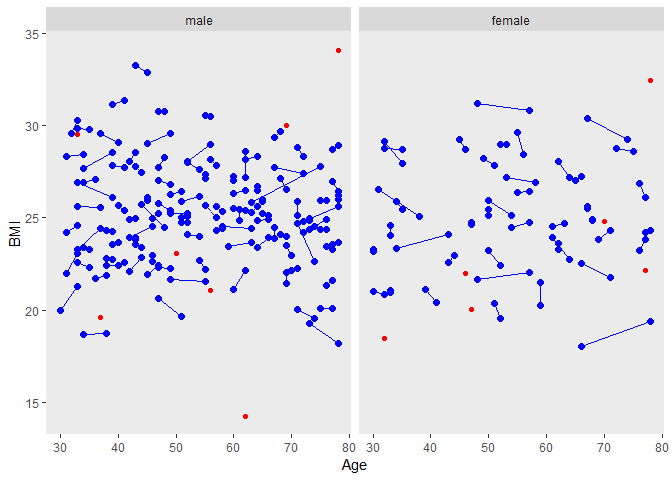
labels <- c("0" = "male", "1" = "female")
ggplot(tt,aes(Age, BMI, group=matnum))+
geom_point(size=2, colour="blue")+
geom_line(colour="blue")+ facet_grid( ~ female, labeller=labeller(female = labels))+
theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank())+
geom_point(data=dused1, aes(Age, BMI, group=matnum),color="red")
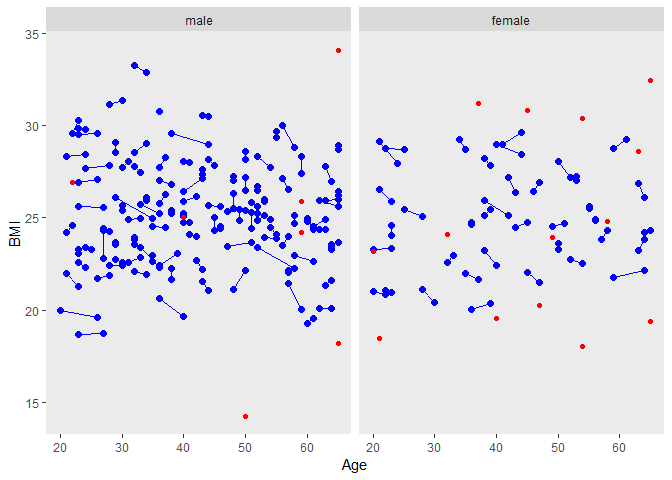
male의 trt vs control group 비교
tt %>% filter(female==0) %>%
group_by(rx) %>%
summarize(count=n(),mu.age=mean(Age),sd.age=sd(Age),mu.BMI=mean(BMI),sd.BMI=sd(Age))%>%
kable()
| rx | count | mu.age | sd.age | mu.BMI | sd.BMI |
|---|---|---|---|---|---|
| 0 | 102 | 42.56863 | 13.08049 | 25.23196 | 13.08049 |
| 1 | 102 | 42.51961 | 13.51620 | 25.21000 | 13.51620 |
female의 trt vs control group 비교
tt %>% filter(female==1) %>%
group_by(rx) %>%
summarize(count=n(),mu.age=mean(Age),sd.age=sd(Age),mu.BMI=mean(BMI),sd.BMI=sd(Age))%>%
kable()
| rx | count | mu.age | sd.age | mu.BMI | sd.BMI |
|---|---|---|---|---|---|
| 0 | 37 | 41.94595 | 13.85028 | 24.88054 | 13.85028 |
| 1 | 37 | 41.62162 | 13.39227 | 24.96757 | 13.39227 |
The distributions of the matching variables (or least the means and standard deviations) appear quite close, as we can see by looking at the males and females separately.
caliper values 에 따른 비교
1. caliper = c(0,0.5,0.5) ⇒ c(0,0.2,0.2)
We could get shorter line segments if we reduced the caliper values, but we would certainly increase the number of unmatched patients.
set.seed(1227)
dsamp <- r_data_frame(n = 300,
id,
sex(x = c(0,1),
prob = c(0.7,0.3),
name = "female"),
age(x = 30:78,
name = 'Age'),
Scoring=rnorm(300,25,3))
colnames(dsamp) <- c("ID","female","Age","BMI")
dsamp$BMI <-round(dsamp$BMI, 2)
dsamp$female <- as.numeric(dsamp$female)-1
dsamp <- dsamp %>% as.data.table()
dsamp[, rx := 0]
dused <- NULL
drand <- NULL
dcntl <- NULL
set.seed(1227)
while (nrow(dsamp) > 1) {
selectRow <- sample(1:nrow(dsamp), 1)
dsamp[selectRow, rx := 1]
myTr <- dsamp[, rx]
myX <- as.matrix(dsamp[, .(female, Age, BMI)])
match.dt <- Match(Tr = myTr, X = myX,
caliper = c(0,0.2,0.2), ties = FALSE)
if (length(match.dt) == 1) { # no match
dused <- rbind(dused, dsamp[selectRow])
dsamp <- dsamp[-selectRow, ]
} else { # match
trt <- match.dt$index.treated
ctl <- match.dt$index.control
drand <- rbind(drand, dsamp[trt])
dcntl <- rbind(dcntl, dsamp[ctl])
dsamp <- dsamp[-c(trt, ctl)]
}
}
drand$matnum <- c(1:dim(drand)[1])
dcntl$matnum <- c(1:dim(dcntl)[1])
dused1 <- dused
dused1$matnum <-NA
tt <- bind_rows(as.data.frame(drand),as.data.frame(dcntl))
labels <- c("0" = "male", "1" = "female")
ggplot(tt,aes(Age, BMI, group=matnum))+
geom_point(size=2, colour="blue")+
geom_line(colour="blue")+ facet_grid( ~ female, labeller=labeller(female = labels))+
theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank())+
geom_point(data=dused1,aes(Age, BMI, group=matnum),color="red")
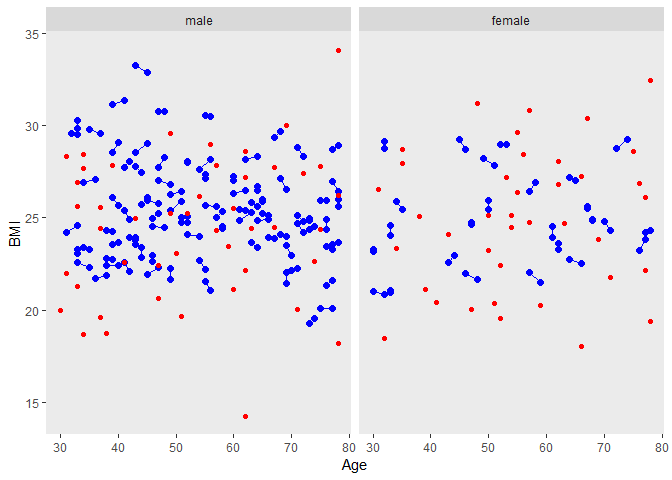
2. caliper = c(0,0.5,0.5) ⇒ c(0,0.9,0.9)